The Inverse Square Law of Bias

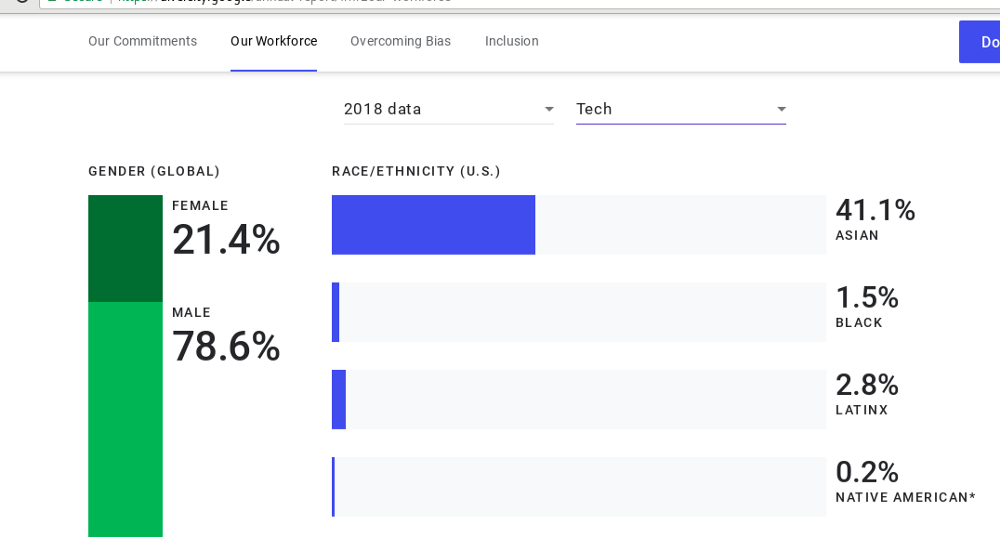
Consider a typical (sadly) tech workplace where there are four men for every woman.$^1$ Assume that women and men both exhibit bias to members of other genders at the same rate. Then women will experience gender bias at a rate of sixteen times more than men.

Yes, a simple mathematical model shows minority experience of bias relative to the majority experience goes up with the square of how underrepresented they are.

To take another example from the tech world, underrepresented minorities (Black, Latinx, Native American) are outnumbered typically at a ratio of twenty to one,$^1$ Again assuming racial bias happens both ways at the same rate, the model shows that the underrepresented minorities will experience racially biased behavior four hundred times more often than members of other groups.

This model could be part of the explanation for why so many members of the majority do not see bias in the workplace$^2$. A white man might not realize that some particular type of bias that he only experiences once a year might be experienced much more frequently by minorities: perhaps more than once a month by his women colleagues and more than once a day by his colleagues from underrepresented minorities.

The model applies to all kinds of biased acts ranging from small acts of exclusion and unconscious bias to full-on racial prejudice and sexual harassment. At every level of severity, it predicts marked increases in the expected frequency of the experienced bias with lower minority representation.

Of course, this model grossly simplifies the real world. Gender and race are not binaries. There are intersectionalities that make things more complex. Biased actions are not uniformly distributed and directed. One implication is that in practice, the ratio of experienced bias might grow a bit slower than the square, but I still think it grows faster than linear.

This squaring relationship is known as the Petrie Multiplier after its discoverer Karen Petrie. It is explained in detail in an article by Ian Gent$^3$.

(Note, I hesitated to publish this article as it reduces painful lived experience to cold impersonal mathematics, and I believe our first reactions to issues of representation and bias in tech should be outrage and a commitment to fix the system. But even as these issues divide us, there is one thing that unites us: we are all engineers, and at least in mathematics we can find a common understanding.)

Appendix

(You can stop reading now if you don't care about the mathematics.)

Assume a population of two disjoint groups of people (majorities and minorities) where there are $k$ majorities for every $1$ minority. Let the total population be $n$, so there are $\frac{n}{k+1}$ minorities and $\frac{n k}{k+1}$ majorities.

Assume that people in each group act in a biased way to individual members of the other group at the same rate $r$ per time period.

Thus in total, majorities perpetrate $\frac{r n k}{k+1}$ acts of bias directed at $\frac{n}{k+l}$ minorities, so each minority is a victim of $r k$ acts of bias.

Conversely, in total, minorities perpetrate $\frac{r n}{k+1}$ acts of bias directed at $\frac{n k}{k+l}$ majority members, so each majority is a victim of $\frac{r}{k}$ acts of bias.

Comparing the rate that minorities experience bias ($r k$) and the rate that majorities experience bias ($\frac{r}{k}$) we see that minorities experience bias at a rate of $k^2$ higher than majorities.

References

$^1$Google diversity annual report

$^2$Why Male Tech Workers Don't See the Gender Gap

$^3$The Petrie Multiplier: Why an Attack on Sexism in Tech is NOT an Attack on Men